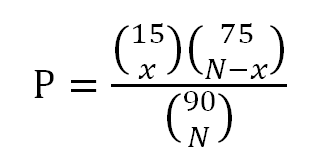Probabilità – infigures

03/02/202419/02/2024

La questione dell’ovetto Kinder

Sei un appassionato collezionista di ovetti Kinder? Ti sei mai chiesto quanti ovetti potresti dover acquistare prima di completare la collezione delle sorprese? In questo articolo, esploreremo la questione dal punto di vista probabilistico in modo da calcolare il numero medio di ovetti necessari per finire la collezione.

Le sorprese Kinder sono divise in collezioni, ognuna con il suo tema, si va dai Minions a Frozen. Ogni periodo dell’anno è caratterizzato dalla sua particolare collezione. Tuttavia, come tutti i bambini hanno imparato a scoprire a proprie spese, non tutti gli ovetti contengono una sorpresa della collezione: solo uno ogni tre! Bene, ora facciamo qualche conto supponendo di essere alla disperata ricerca di finire la collezione di Frozen.

La collezione di Frozen è composta da 8 personaggi. Anzitutto ci domandiamo: quanti ovetti mi aspetto di dover comprare per ottenere tutte e 8 le soprese della collezione di Frozen? Questo è il classico esempio del problema del collezionista. Tralasciando questioni troppo tecniche legate al calcolo delle probabilità, il numero medio di ovetti che ci si aspetta di dover comprare è calcolabile tramite questa semplice formula:

$N = 3 * 8 * ( \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{8} ) \approxeq 65$

Chiaramente questo rappresenta solamente un numero medio, una sintesi estrema. In altre parole, non ho alcuna certezza di finire la collezione con 65 ovetti. Di fatto, ci saranno persone che finiscono la collezione con una decina di ovetti (non è il mio caso!) e altri che pur avendone comprati 100 non l’hanno ancora finita.

A ben vedere dunque, ogni persona finisce la collezione entro un certo numero di ovetti in base alla propria fortuna o sfortuna (agli statistici piace chiamarlo caso ma non sappiamo essere semplicemente questione di sfiga!).

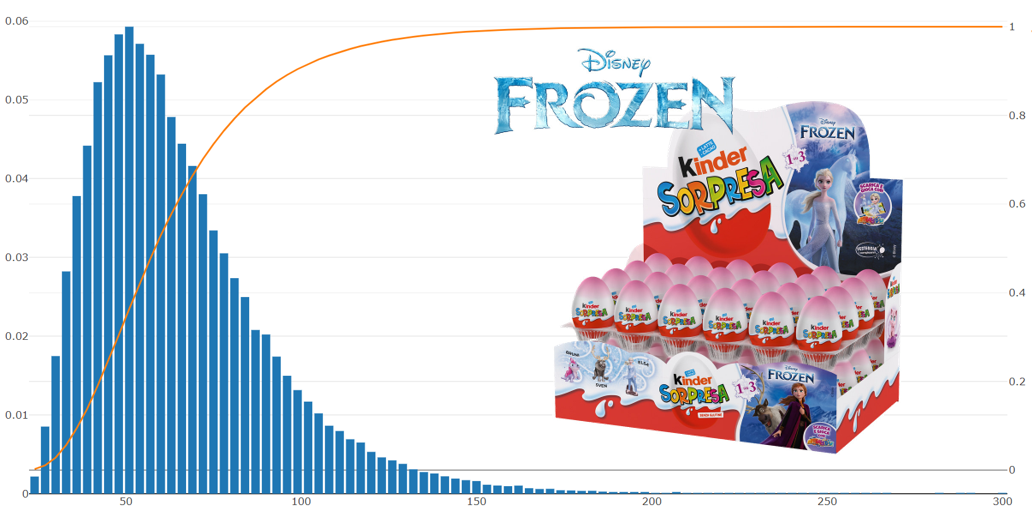
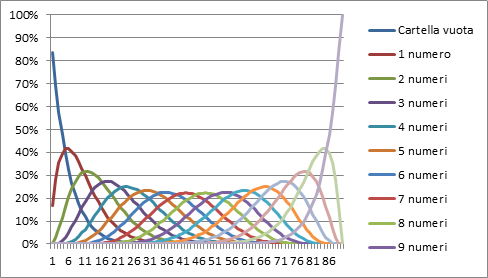
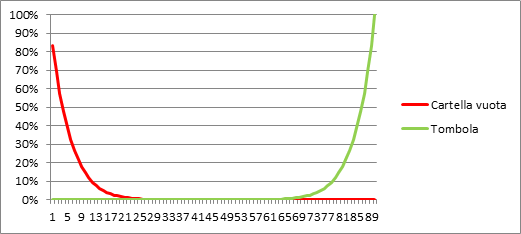
Da un punto di vista probabilistico, ad ogni numero di ovetti comprati è possibile associare una probabilità di aver finito la collezione. Ad esempio è possibile calcolare la probabilità di finire la collezione avendo comprato esattamente 50 ovetti, oppure la probabilità di averne comprati esattamente 90. Calcolare la probabilità per ciascuno di questi valori vuol dire aver costruito quella che viene chiamata la curva di distribuzione della nostra variabile aleatoria. Per studiare questa distribuzione, abbiamo condotto una simulazione di 100mila casi e questi sono i risultati:

Clicca qui per allargare il grafico.

Ogni barra blu rappresenta la probabilità di finire la collezione avendo comprato un determinato numero di ovetti. La curva in arancione invece rappresenta la probabilità di completare la collezione entro un certo numero di ovetti (viene chiamata cumulata). Ad esempio la probabilità di finire la collezione entro 100 ovetti è di circa il 90%. In altre parole comprare 100 ovetti non mi mette al riparo da quel 10% di sfiga sempre lì pronto ad attendermi.

Per i più appassionati:
Se sei un appassionato collezionista di ovetti Kinder, condividi la tua esperienza nei commenti! Quanti ovetti hai dovuto acquistare per completare la tua collezione?

Per i più nerd:
Il grafico è stato costruito in R utilizzando le librerie ggplot2 e plotly. Se sei interessato ai dettagli tecnici e vuoi esplorare il codice dietro questa visualizzazione, non esitare a chiedere!

13/12/202219/02/2024

Tombola e probabilità

Natale è alle porte e c’è già chi mette da parte un congruo ammontare di monete e bucce di mandarino per affrontare al meglio le roboanti partite a tombola in programma per le prossime settimane. Tombolate che si prospettano decisamente più agguerrite dei Mondiali di calcio in Qatar. Oggi come al solito parliamo di numeri, più in particolare di probabilità. Probabilità legate al gioco della tombola.

Pagine: 1 2

22/12/201919/02/2024

Tombolata natalizia

Natale. Tempo di regali, presepi, addobbi, alberi, famiglia e …tombolate! Ed è proprio della tombola che parleremo oggi. Un gioco che si presta molto bene a tanti quesiti di natura probabilistica. Ad esempio: Qual è la probabilità di mettere un numero sulla cartella già alla prima estrazione? Qual è la probabilità di fare ambo dopo due estrazioni? Qual è la probabilità di fare ambo entro le prime 10 estrazioni? E terno? Dopo quante estrazioni è più probabile fare tombola? Quante cartelle conviene comprare? È meglio prendere il tabellone o sei cartelle?

Proviamo a dare risposta ad alcuni di questi interrogativi, pur nella consapevolezza che non aumenteranno le vostre probabilità di vincita.

Cominciamo da una domanda facile facile: qual è la probabilità che alla prima estrazione esca un numero presente sulla mia cartella? Nonostante la domanda non richieda formule complicate o nozioni di calcolo combinatorio, a volte sento dire 1 su 90 . Sbagliato. Ogni cartella ha 15 numeri pertanto alla prima estrazione la probabilità che venga estratto un numero presente sulla mia cartella è di 15/90. Ovvero circa il 17%.

Si ricorda se mai ce ne fosse bisogno che una cartella della tombola è composta da 15 numeri suddivisi in tre differenti righe e che questi numeri non si ripetono all’interno della cartella stessa.

Altra domanda: qual è la probabilità che con la mia cartella faccia ambo già alla seconda estrazione? La probabilità è bassa ma non bassissima: (15/90)*(4/89) circa 0.7% ovvero una probabilità su 133.

Che poi ci sia il simpaticone di turno che grida “ambo!” già alla prima estrazione, beh quello è un altro discorso. La probabilità di trovare il simpaticone in un gruppo di N elementi ce la conserviamo come esercizio per la prossima volta.

Possiamo generalizzare la domanda in questo modo: qual è la probabilità che dopo N estrazioni la mia cartella contenga esattamente X segnalini? Dove per X si intende un numero da 0 a 15. (0 cartella ancora vuota e 15 tombola). E dove per ‘segnalini’ si intendono bucce di mandarino, fagiolini,… a seconda delle usanze locali e le preferenze personali. In formule:

Ma piuttosto che far parlarle le formule, diamo spazio al grafico:

Nota importante: con X=2 non si intende la probabilità di fare ambo, quanto piuttosto la probabilità di una cartella con esattamente due segnalini (non necessariamente sulla stessa riga). Per la cronaca, la probabilità che essendoci due segnalini sulla cartella questi si trovino sulla stessa riga (ambo)è pari a 4 su 14 (ovvero circa 28%). Allo stesso modo X=3 non significa aver fatto terno, né x=4 quaterna e né x=5 cinquina. Però X=15 equivale ad aver fatto tombola! (vedi i dati in tabella)

Ora soffermiamoci su due curve in particolare.

La curva (in rosso) che descrive la probabilità di avere una cartella vergine ad una certa estrazione decresce molto velocemente. Dopo 12 estrazioni scende sotto al 10% e dopo 22 estrazioni scende sotto all’1%. Al contrario la probabilità di fare tombola con una certa cartella (curva in verde) cresce molto lentamente all’aumentare delle estrazioni. Dopo 68 estrazioni rimane di circa l’1% mentre è del 50% alla 86-esima estrazione. Teniamo a mente il fatto che queste sono le probabilità per una determinata cartella. È chiaro che il verificarsi della tombola (da parte di un qualsiasi giocatore) nel corso di una partita dipende dal numero di cartelle in gioco. In particolare:

Ora prendiamo in considerazione Paperino e Gastone rispettivamente il papero più sfortunato e quello più fortunato sulla faccia di Paperopoli.

Paperino estrazione dopo estrazione non riesce a mettere nessun numero sulla sua cartella. Arriva alla 75 esima estrazione e la sua cartella rimane vuota! Una probabilità dello 0.000000000000002%; detto in altri termini una probabilità su 45,795,673,964,460,800 (oltre 45 biliardi). Questa è la stessa probabilità che ha Gastone di fare tombola con la sua cartella dopo appena 15 estrazioni. Il termine tecnico per definire tale probabilità è “culo esponenziale”.

Ma andiamo avanti. Abbiamo visto le percentuali esatte della tombola e di quanti numeri posso aspettarmi di aver riempito la mia cartella dopo N estrazioni ma ancora rimane da rispondere alla domanda: qual è la probabilità di fare ambo entro N estrazioni? E terno, quaterna e cinquina? Per rispondere a queste domande ho effettuato una simulazione con 10mila partite. Il grafico sottostante mostra la probabilità di fare ambo terno,… prima della N-esima estrazione (con N da due a 90).

Da questo possiamo desumere il numero medio di estrazioni che dobbiamo attendere prima che la nostra cartella si verifichi un ambo, un terno, una quaterna, una cinquina e una tombola.

	Ambo	Terno	Quaterna	Cinquina	Tombola
Numero medio di estrazoni	15	29	46	65	86

Queste però sono le probabilità per una singola cartella. Ma la tombola non è un solitario. Il bello del gioco è proprio quello di giocare in tanti. Maggiore è il numero dei giocatori/cartelle e prima si verificheranno le vincite.

Passiamo ad un altro domandone che assilla i tombolisti veraci: conviene prendere il tabellone o sei cartelle? Sebbene la probabilità di vincita di una determinata cartella e una del tabellone sia uguale, le sei cartelle che formano il cartellone hanno una caratteristica importante rispetto a sei cartelle prese a caso: ciascun numero compare una e una sola vota. Prendendo invece sei cartelle a caso ci saranno numeri doppi, alcuni anche tripli e numeri che non sono presenti in nessuna cartella. Questa particolarità del cartellone lo avvantaggia quando si considera la probabilità di fare tombola. Questa “supremazia” del tabellone è stata dimostrata sia teoricamente da Roberto Natalini (ricercatore del CNR – leggi articolo) che verificata da simulazioni condotte. A questo indirizzo potrete trovare un simulatore molto ben fatto, progettato da Luca Rainone che illustra visivamente questo fenomeno. Il vantaggio della cartellonista è comunque limitato 54% contro 46%.

Per ovviare a questa seppur minima supremazia del tabellone occorre procurarsi delle cartelle che godano anch’esse della caratteristica di non avere numeri ripetuti. Sembra un compito complicato ma in verità i fabbricanti di tombole ci vengono in aiuto. Ogni cartella ha un suo proprio numero progressivo. Occorrerà semplicemente prendere cartelle in serie.

Non mi resta che augurarvi buone feste e felici tombolate!

13/10/201519/02/2024

Il “paradosso” del compleanno

Ho sempre avuto un debole per i paradossi della logica ma quello di cui vorrei parlare oggi, il celebre “paradosso” dei compleanni, in verità non è un vero paradosso in senso stretto. È piuttosto un verità matematica che contraddice l’intuizione comune. Ma vediamo meglio di cosa stiamo parlando. Provate a chiedere ad un vostro amico questa semplice domanda:

“Qual è la probabilità che in una classe di 23 studenti almeno due festeggino il compleanno lo stesso giorno?”

Sia chiaro, non cerchiamo una risposta esatta quanto piuttosto un valore indicativo:

molto molto improbabile (<1%)
molto improbabile (<5%)
poco probabile (meno del 10%)
così così (circa 50%)
abbastanza probabile (circa 75%)
molto probabile (>90%)

Ebbene, statene pur certi, la stragrande maggioranza dei vostri amici vi risponderà che la probabilità è molto bassa. In verità, calcoli alla mano, la reale percentuale è pari al 51%. Non ci credete? Provate allora a considerare dei casi pratici tra i colleghi del vostro ufficio, tra la cerchia delle vostre amicizie, tra i compagni di scuola di vostro figlio. Vi accorgerete che le cose stanno proprio così. La probabilità che due persone in un gruppo compiano gli anni nello stesso giorno è molto superiore a quanto il nostro intuito ci porterebbe a considerare. Qui di seguito il grafico che illustra l’andamento della probabilità al crescere del numero di persone nel gruppo.

Per chi fosse interessato alla matematica dietro a questo problema si inizia calcolando la probabilità che tutti gli studenti siano nati in giorni diversi e poi si calcola il suo complemento, in formule:

$P(p) = 1-\frac{364!}{365^{p-1}(365-p)!}$

La bellezza del “paradosso del compleanno” sta nel mettere a nudo i limiti della nostra intuizione. Intuizione che spesso ci aiuta a vedere le cose con un “terzo occhio” ma che a volte incorre in questi clamorosi errori di valutazione!